| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- PriorityQueue
- 2020
- intarray
- report
- 알고리즘
- Queue
- heap
- sortedBy
- lastIndex
- Util
- booleanarray
- 코틀린
- indices
- Java
- GREEDY
- dynamic programming
- 동적계획법
- Kotlin
- hackerrank
- Developer
- Poll
- solution
- foreach
- Recursion
- contentToString
- programmers
- dp
- Main
- 2D Array
- 프로그래머스
- Today
- Total
Code in
탐욕 알고리즘 Greedy Algorithm + A* Search Algorithm 본문
탐욕 알고리즘 Greedy Algorithm
그리디 알고리즘은 동적 프로그래밍을 할 때 지나치게 많은 일을 하는 것을 보다 효율적으로 바꾸기 위해서 생겨난 알고리즘입니다. 따라서 동적 프로그래밍과 함께 쓰였을 때 서로 보완할 수 있습니다.
Greedy Algorithm은 탐욕 알고리즘, 욕심쟁이 알고리즘으로 불립니다.
매 순간 최선의 선택을 하여 최종적으로 최선이 되도록 하는 알고리즘입니다.
매 순간 해당 순간을 위한 최선의 선택만을 하기 때문에 미래에 어떤 영향을 줄지는 생각하지 않습니다.
모든 경우에 그리디 알고리즘이 적합하진 않지만, 몇몇 케이스에서는 그리디 알고리즘으로 최종적으로 최선인 답을 보다 효율적으로 구할 수 있습니다.
요약하면,
1. 동적 계획법과 마찬가지로 최적화 문제를 푸는 데 사용되고
2. 근시안적으로 해당 순간에 가장 최적인 해를 구하기 때문에
3. 동적 계획법보다 효율적이지만 모든 경우에 최적의 해는 아닐 수 있습니다.
알고리즘 구현
1. 최선의 선택: Selection Procedure, 해당 순간의 최적인 해를 구하여 이를 부분해 집합에 추가합니다.
2. 적절성 검사: Feasibility Check, 부분해 집합이 적절한지 검사합니다.
3. 최종해 검사: Solution Check, 부분해 집합이 문제의 해가 되는지 검사합니다.
4. 문제의 해가 완성되지 않았다면 1번부터 다시 시작합니다.
이러한 그리디 알고리즘은
프림 알고리즘과 크루스 칼 알고리즘, 다익스트라 알고리즘, Minimum Spanning Trees, Huffman Coding, Travelling Salesman Problem, Scheduling Problem, A* Search Algorithm 등에 사용됩니다.
A* Search Algorithm
A* Search Algorithm은,
지도 등에서 방해물이 많을 때 가장 짧은 경로를 찾기 위해서 고안되었습니다.

경로 탐색을 위한 알고리즘으로 자주 사용됩니다.
사진처럼 출발 지점에서 도착 지점까지 많은 방해물이 있고 사각형 Grid로 구분하는 상황을 생각했을 때, A* Search Algorithm을 사용할 수 있습니다.
매 순간 Step 마다 가장 작은 ' f ' 값을 찾아 다음 노드를 선택합니다.
이때 ' f ' 값은 ' g ' 값과 ' h ' 값의 합입니다.
' g '는 시작 지점에서 주어진 해당 지점까지 생성된 경로에 대한 이동 비용 Cost입니다.
' h '는 Heuristic으로, 주어진 해당 지점에서 도착 지점까지의 이동 비용 Cost입니다.
Heuristic은 잘 추측하는 기술 art of good guessing으로, 그리디 알고리즘처럼 해결책의 발견을 보장하지는 않지만 가능성이 없는 대안책을 시도하지 않고도 배제할 수 있습니다. 방해물들이 많기 때문에 실제 거리를 알지 못하지만, 이러한 ' h '를 계산하는 방법은 다양합니다.
알고리즘 구현 방법
: Open List와 Closed List를 사용합니다. ( Dijkstra Algorithm처럼 )
1. Open List를 선언합니다.
2. Closed List를 선언합니다. Open List에 시작 노드를 추가합니다. 이 때 f 값은 0으로 할 수 있습니다.
3. Open List가 비어있지 않을 경우 다음을 반복합니다.
a. Open List에서 ' f ' 값이 가장 작은 노드를 찾아 ' q '라고 명칭 합니다. // 주어진 해당 지점
b. ' q '를 Open List에서 제거 pop 합니다.
c. ' q '를 부모로 하는 노드 8개를 생성합니다. // 3x3에서 가장 가운데가 q라서 8개의 노드가 필요합니다.
d. 각각의 8개 노드에 대해서,
aa. 만약 해당 노드가 목표 노드라면 탐색을 멈추고,
해당 노드. g = q.g + distance( 해당 노드와 q 사이의 거리 )
해당 노드. h = distance( 해당 노드와 목표 노드 사이의 거리 )
해당 노드. f = 해당 노드. g + 해당 노드. h
bb. 만약 해당 노드와 같은 위치를 가진 노드가 Open List에 있고,
Open List에 있는 노드의 ' f ' 값이 더 작다면, 해당 노드를 skip 합니다.
cc. 만약 해당 노드와 같은 위치를 가진 노드가 Closed List에 있고,
Closed List에 있는 노드의 ' f '값이 더 작다면, 해당 노드를 skip 하고
Closed List에 있는 노드를 Open List에 추가합니다.
e. 'q'를 Closed List에 추가합니다.
아래 그림처럼, Soruce에서 Target까지의 경로를 구하려고 할 때 A* Search Algorithm을 사용할 수 있습니다.
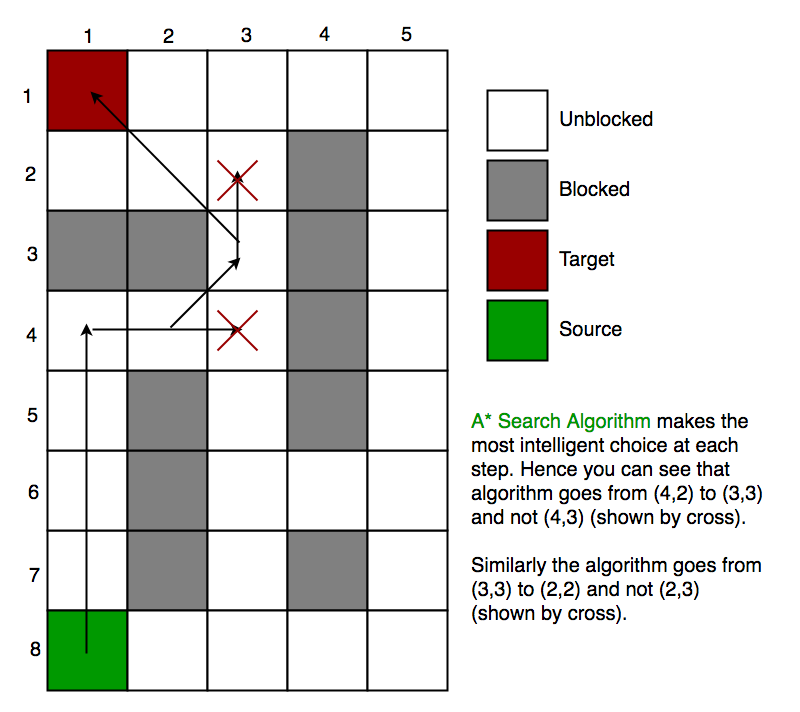
Heuristics
1. h의 정확한 값을 측정하거나
2. 다른 heuristics를 사용해서 h의 값을 추측하여
' h '의 값을 구할 수 있습니다.
1번 방법을 위해서는 A* Search Algorithm 이전에 모든 거리를 미리 계산하거나,
방해물이 없다면 Distance Formula / Euclidean Distance를 사용하여 정확한 값을 찾을 수 있습니다.
2번 방법을 위해서는 3가지의 추측 heuristics가 있습니다.
a. Manhattan Distance
-
목표 위치까지의 x, y 좌표들의 각각의 차이에 대한 절댓값의 합입니다.
-
상하좌우 4 방향으로만 움직일 수 있을 때 사용합니다.
h = abs (current.x - goal.x) + abs (current.y - goal.y)
b. Diagonal Distance
-
목표 위치까지의 x, y 좌표들의 각각 차이에 대한 절댓값의 최댓값입니다.
-
8 방향으로 움직일 수 있을 때 사용합니다. - 체스의 king의 이동과 유사합니다.
h = max { abs(current.x – goal.x), abs(current.y – goal.y) }
c. Euclidean Distance
-
목표 위치까지의 x, y 좌표들의 거리를 Distance Fomula을 사용하여 구한 값입니다.
-
어느 방향으로든 움직일 수 있을 때 사용합니다.
h = sqrt ( pow ( (current_cell.x – goal.x), 2 ) + pow ( (current_cell.y – goal.y), 2 ) )
또한,
-
모든 노드의 ' h ' 값이 0일 경우, Dijkstra 알고리즘과 유사하게 작동합니다.
-
피보나치 힙을 사용하면 성능이 향상되며, 동적 프로그래밍을 사용하면 계산 시간이 줄어들 수 있습니다.
-
그리디 알고리즘을 사용하였고 경험적 접근/근사치 등 추측을 사용하기 때문에 항상 최단 경로를 생성하지는 않지만 대부분의 경우 경로 탐색을 성공적으로 수행합니다.
-
검색하는 공간이 Grid가 아닌 Graph여도 적용이 가능합니다.
이 외에도 경로 탐색 알고리즘의 경우,
1) 하나의 소스, 하나의 목적지일 때
A* Search Algorithm 사용 ( 비가중, 가중 그래프 )
2) 하나의 소스, 모든 목적지일 때
BFS ( 비가중 ), Dijkstra ( 음수 가중치가 없는 가중 ), Bellman Ford ( 음수 가중치가 있는 가중 )
3) 모든 노드 사이에서
Floyd-Warshall, Johnson’s Algorithm
을 사용할 수 있습니다.
출처: https://www.geeksforgeeks.org/a-search-algorithm/
A* Search Algorithm - GeeksforGeeks
A* Search algorithm is one of the best and popular technique used in path-finding and graph traversals.
www.geeksforgeeks.org
'알고리즘 스터디_개념정리' 카테고리의 다른 글
| 깊이 우선 탐색 DFS, 너비 우선 탐색 BFS (0) | 2020.08.23 |
|---|---|
| 동적 계획법( DP - Dynamic Programming ), 메모이제이션( Memoization ) (0) | 2020.08.23 |
| 완전 탐색 알고리즘 - Brute Force (1) | 2020.08.17 |
| 스택, 큐, 힙 (0) | 2020.08.10 |
| 정렬 알고리즘 (0) | 2020.08.10 |


