| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- dp
- programmers
- solution
- 코틀린
- intarray
- Main
- lastIndex
- contentToString
- Recursion
- Util
- heap
- Developer
- 알고리즘
- Java
- hackerrank
- indices
- Kotlin
- Queue
- foreach
- 2D Array
- GREEDY
- PriorityQueue
- 동적계획법
- 2020
- booleanarray
- Poll
- sortedBy
- 프로그래머스
- dynamic programming
- report
- Today
- Total
Code in
깊이 우선 탐색 DFS, 너비 우선 탐색 BFS 본문
깊이 우선 탐색 DFS, 너비 우선 탐색 BFS에 앞서서
사용되는 자료구조인 그래프에 대해서 알아보겠습니다.
그래프
-
노드 Node와 노드를 연결하는 간선 Edge을 하나로 모아놓은 비선형 자료구조
-
연결된 객체 간의 관계를 표현하는 자료구조
-
정점 vertex와 간선 edge로 이루어진 자료구조 G = (V, E)
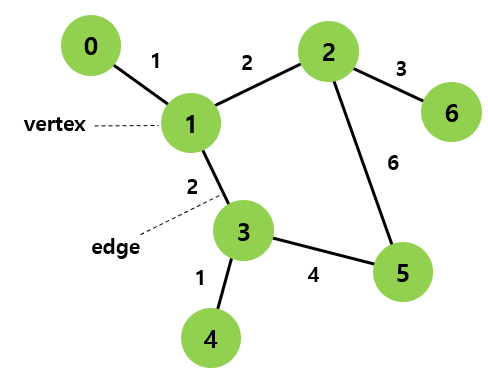
흔히 이야기하는 트리 구조는 조건들이 추가된 그래프의 일종입니다.
그림과 같이 표시된 방향이 없는 무방향 그래프도 있지만, 방향이 표기된 방향 그래프도 존재합니다.
그래프 탐색
하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것입니다.
깊이 우선 탐색 DFS와 너비 우선 탐색 BFS도 그래프 탐색의 한 종류입니다.
두 방식 모두 그래프 G = (V, E)의 모든 간선을 조회하기 때문에 다음 시간 복잡도를 가지고 있습니다.
인접 리스트로 표현된 그래프는 O(V+E)
인접 행렬로 표현된 그래프는 O(V^2)
일반적으로 간선(E)의 개수가 노드(V)의 개수보다 적기 때문에 인접 리스트 방식이 더 효율적입니다.
-
모든 정점을 방문하는 것이 중요한 문제는 DFS, BFS 둘 모두 사용 가능합니다.
-
경로의 특징을 저장해야 하는 문제는 DFS를 사용합니다. 경로의 특징은 DFS에서 가질 수 있기 때문입니다.
-
최단 거리를 구해야 하는 문제는 BFS를 사용합니다. BFS에서는 가까운 곳부터 찾기 때문입니다.
-
검색 대상 그래프의 규모가 크다면 DFS를 사용합니다.
-
검색 대상 그래프의 규모가 크지 않고 원하는 대상이 검색 시작 지점에서 멀지 않다면 BFS를 사용합니다.
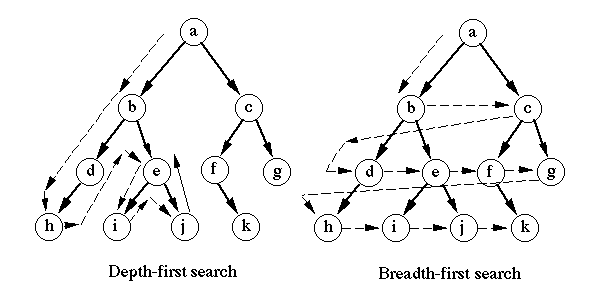
깊이 우선 탐색 DFS - Depth-First Search
DFS는 특정 노드에서 시작하여 해당 가지(분기, Branch)를 끝까지 탐색한 다음 가지로 이동하여 탐색하는 방법입니다. 넓게 탐색하기 전에 깊게 탐색하는 방법으로, 모든 노드를 방문하고자 하는 경우에 사용되며 BFS에 비해 간단하지만 속도가 더 느립니다.
자기 자신을 호출하는 순환 알고리즘의 형태를 가지고 있으며, 어떤 노드를 방문했었는지에 대한 것을 저장하고 확인해야만 합니다. 그러지 않으면 무한루프에 빠질 수 있습니다.
이러한 DFS는 스택 혹은 재귀 호출을 사용하여 구현할 수 있습니다.
-
Stack에 있는 Top 노드에 대하여 더 연결되는 노드가 있는지 확인합니다.
-
계속해서 연결되는 노드가 이어진다면 Stack에 방문한 노드를 삽입합니다.
-
더 이상 이어진 노드가 없다면, 해당 데이터를 Stack에서 제거하여 다음 데이터가 Top에 오도록 합니다.
너비 우선 탐색 BFS - Breath-First Search
특정 노드에서 시작하여 인접한 노드를 먼저 탐색하는 방법입니다. 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 보다 나중에 방문하는 방법입니다. 깊게 탐색하기 전에 넓게 탐색하는 방법으로, 두 노드 사이의 최단 경로 혹은 임의의 경로를 찾을 때 사용됩니다.
재귀적으로 동작하지 않으며, DFS와 마찬가지로 어떤 노드를 방문했었는지에 대한 것을 저장하고 확인해야만 합니다. 그러지 않으면 무한 루프에 빠질 수 있습니다.
이러한 BFS는 방문한 노드들을 차례로 저장한 후 꺼낼 수 있는 큐 Queue를 사용합니다. (선입선출 FIFO)
깊이가 1인 모든 노드를 방문한 다음 깊이가 2인 모든 노드를 방문, 깊이가 3인 모든 노드를 방문하는 식으로 계속해서 방문하며 더 이상 방문할 곳이 없으면 탐색을 끝냅니다.
** 깊이는 시작 노드에서 해당 노드까지 접근할 때 거쳐가는 연결된 간선의 개수와 비슷한 개념으로 이해할 수 있습니다. 첫 번째 노드에서 해당 노드까지 가는 경로에 존재하는 간선의 개수가 1이면 깊이가 1입니다.
'알고리즘 스터디_개념정리' 카테고리의 다른 글
| 이진 탐색 Binary Search (1) | 2020.08.30 |
|---|---|
| 해시 알고리즘 (1) | 2020.08.30 |
| 동적 계획법( DP - Dynamic Programming ), 메모이제이션( Memoization ) (0) | 2020.08.23 |
| 탐욕 알고리즘 Greedy Algorithm + A* Search Algorithm (1) | 2020.08.17 |
| 완전 탐색 알고리즘 - Brute Force (1) | 2020.08.17 |



