| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 2020
- Kotlin
- foreach
- intarray
- dp
- programmers
- dynamic programming
- Java
- booleanarray
- Developer
- solution
- heap
- Main
- hackerrank
- contentToString
- Queue
- 알고리즘
- 2D Array
- 코틀린
- PriorityQueue
- GREEDY
- indices
- 프로그래머스
- sortedBy
- report
- lastIndex
- Recursion
- 동적계획법
- Util
- Poll
- Today
- Total
Code in
정렬 알고리즘 본문
Sorting 정렬 알고리즘
: N개의 숫자를 입력받아서 오름차순ASC 혹은 내림차순DESC으로 정렬하여 출력하는 알고리즘이다.
* 오름차순: ASC, Ascending **내림차순: DESC, Descending
간략하게는,
Swap을 주로 사용하는 선택 정렬과 버블 정렬,
중간에 데이터를 삽입하여 그 뒤의 데이터들의 위치를 바꾸는 삽입 정렬과 쉘 정렬
분할 정복을 사용하는 합병 정렬과 퀵 정렬, Tim Sort, Intro Sort
버킷을 사용하는 기수 정렬과 버킷 정렬, Counting Sort
최대 힙을 사용하는 힙 정렬 등이 있다.
*임의로 크게 나누었을 때이므로 세부적으로는 차이가 있다.
이 때, 입력 데이터들 중 같은 값들이 존재할 때 정렬 과정에서 이들의
위치가 바뀌지 않을 경우 안정 정렬이라 한다.
이러한 안정 정렬에는 버블, 삽입, 합병, Tim Sort 등이 있다.
▶ 선택 정렬 Selection Sort
시간복잡도는 배열의 구성과 상관없이 전체 비교를 진행하기 때문에,
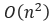
매번 정렬되지 않은 모든 데이터들 중 최소/최대 값을 비교하여 얻어낸 다음 해당 값을 알맞은 위치의 값과 Swap한다. 위치의 경우, 가장 앞쪽부터 차례대로 정렬해 나가기 때문에 매번 알맞은 위치가 정해져 있다.
1. 위치index를 선택한다. (정렬되지 않은 데이터들 중 가장 앞쪽 값의 위치를 선택한다.)
2. 정렬되지 않은 데이터들을 전부 검사하여 가장 작은 값을 찾는다.
3. 가장 작은 값을 위치index의 값과 Swap한다.
4. 위의 과정을 반복한다. (index가 끝에 다다를 때까지 반복한다.)
| 3 (A) |
1 (min) |
7 | 5 | 9 |
▶ 버블 정렬 Bubble Sort
시간복잡도는 최선의 경우 비교만 진행하고 Swap하지 않지만, 최악의 경우 둘 모두를 진행하기 때문에,
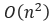
매번 연속된 index의 두 데이터를 비교, Swap하여 정렬한다. 오름차순의 경우는 반복적으로 가장 큰 값이 가장 뒤로 이동하게 된다. 지역이동Local move을 한다.
1. 위치 index를 설정한다. 현재를 A라고 할 때 A+1의 값을 비교한다.
2. A의 값이 더 클 경우 A+1과 Swap하지만 아닐 경우 A의 값을 증가시켜 반복한다.
3. 위의 과정을 (전체 배열의 크기 N - 현재까지 순환한 바퀴 횟수) 만큼 반복한다.
| 3 (A) |
1 (B) |
7 | 5 | 9 |
▶ 삽입 정렬 Insertion Sort
시간복잡도는 이미 정렬된 상태일 때 최선의 시간복잡도가 나오지만, 최악의 경우 역순으로 정렬된 상태이기 때문에,
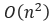
삽입을 진행하기 때문에 삽입된 위치 뒤의 데이터들이 전체 이동을 하게 되어 많은 이동이 이루어진다.
1. 위치 index를 설정한다. 현재를 B라고 할 때 비교할 위치index를 A =B-1로 시작한다.
2. A와 B를 비교한다. B의 값이 더 작으면 B의 값을 A의 앞으로 삽입하기 위해 A를 포함하여 B 이전에 있는 모든 값들을 한칸 뒤로 이동한다. 이후 A의 자리에 B를 삽입한다. 아닐 경우 B의 값을 증가시켜 반복한다.
| 3 (A) |
1 (B) |
7 | 5 | 9 |
▶ 쉘 정렬 Shell Sort
시간복잡도는 간격에 따라 결정된다. 삽입정렬과 마찬가지이므로 정렬일 때 최선의 시간복잡도가 나오지만 최악일 때
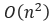
삽입정렬의 최대 문제점인 요소들이 삽입될 때 인접한 위치로만 이동한다는 점을 보완한 알고리즘이다. 전체의 리스트가 한 번에 정렬되지 않으며, 일정한 간격으로 부분 리스트를 생성하여 각 부분 리스트를 삽입 정렬하는 방식이다. 이 떄의 간격은 지속적으로 감소한다. 간격의 수열이 서로소가 되도록 정의하면 성능이 좋아진다. (ex 701, 301, 132, 57, 23, 10, 4, 1)
1. 간격gap K를 설정한다. K는 대부분의 경우 데이터의 크기 N/2이다. 생성된 부분 리스트의 개수는 K와 같다.
2. 각 부분 리스트를 삽입 정렬하여 정렬한다.
3. 각 회전마다 간격 K를 절반으로 줄인다. 이때 홀수로 하는 것이 좋으므로 짝수가 나오면 +1을 한다.
4. 간격 K가 1이 될 때까지 반복한다.
| 7 (A) |
5 (B) |
3 (A) |
1 (B) |
9 (A) |
▶ 합병 정렬 Merge Sort
분할 시의 시간복잡도는 logN이고 합병 시의 시간복잡도는 N이다. 각 분할마다 합병이 진행되므로 시간복잡도는
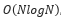
배열의 크기가 1보다 작거나 같을 때까지 2개의 균등 크기로 분할한다. 각 분할마다 재귀적으로 합병 정렬하는 과정을 반복한다. 데이터 크기만큼의 외부 메모리가 필요하다. 데이터의 초기 상태에는 별로 영향을 받지 않는다.
1. 분할한다. 분할 위치는 각 배열의 (처음+끝)/2를 기준으로 한다.
2. 합병한다. 두 배열을 A, B라고 할 때 각각의 첫번째 주소를 a, b라 한다.
3. A[a], B[b]를 비교하여 작은 값을 새 배열 C에 저장한다. A[a]의 값을 C에 저장했을 경우 a++을 한다.
4. a, b가 각 배열의 끝에 도달할 때까지 반복한다.
5. 아직 저장되지 않고 남아있는 배열의 값들을 C에 순서대로 저장한다.
6. 전부 합병되어 C 1개의 배열만 남으면 C배열을 원래 배열에 저장한다.
| 7 (A) |
5 (A) |
3 (B) |
1 (B) |
9 (B) |
▶ 퀵 정렬 Quick Sort
시간복잡도는 배열이 이미 정렬되어있는 최악의 경우에는 크지만 평균적으로는
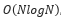
임의의 값 Pivot을 기준으로 작은 값은 왼쪽으로, 큰 값은 오른쪽으로 나누는 Partition하며, 이러한 과정을 양쪽에서 재귀적으로 반복한다. Pivot의 위치가 매우 중요하며 Partition된 배열의 크기가 1이면 정렬이 완료되었다고 할 수 있다. 분할과 동시에 정렬을 진행하며 비교는 배열의 크기N만큼 진행되고, 총 분할 깊이인 logN만큼 비교된다. 최악의 경우를 방지하기 위해 Pivot값을 중간값 혹은 랜덤 값으로 정한다.
1. 가장 왼쪽에 있는 값을 Pivot으로 설정한다. 왼쪽에서 진행하여 pivot보다 큰 수를 left변수로, 오른쪽에서 진행하여 pivot보다 작은 수를 right변수로 설정한다. 두 값을 swap한다.
2. left와 right의 값이 교차하면 swap하지 않고 Pivot과 Pivot보다 작은 값을 swap한다. Pivot을 기준으로 왼쪽은 작은 값들이, 오른쪽은 큰 값들이 모이게 된다.
3. 기존 Pivot을 기준으로 양 쪽을 각각 다시 Quick Sort한다.
| 7 (Pivot) |
9 (left) |
3 (right2) |
8 (left2) |
5 (right) |
▶ Tim Sort
시간복잡도는 평균적으로
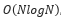
합병 정렬일 때 요소수가 적은 경우 느려지는 것을 개선한 알고리즘이다. 미리 어느 정도의 크기의 정렬이 끝난 열(run)로 분할하고 병합한다. 열run은 32보다 작게 하여 2분할 삽입 정렬을 진행한다.
▶ Intro Sort
시간복잡도는 평균적으로
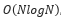
퀵 정렬에서 최악의 경우에 대처하기 위해 recursion depth가 logN을 넘으면 힙 정렬로 바꾼다. 32미만의 데이터 수의 경우는 오버헤드를 적게하기 위해 삽입 정렬로 바꾼다. 하이브리드 정렬 알고리즘이다.
▶ 기수 정렬 Radix Sort
시간복잡도는 버킷의 개수가 K일 때 NK이지만, N이 클 경우 K값이 무시될 수 있으므로
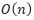
데이터를 특정 진수Radix의 자릿수 별로 정렬한다. 10 Radix에서는 1의 자리, 10의 자리, 100의 자리의 순서로 정렬한다. Radix의 크기만큼의 메모리가 추가로 필요하다. 부동 소수점, 음수값과 같은 특수한 비교 연산은 불가능하다.
▶ Bucket Sort
시간복잡도는 최악의 경우는 크지만, 평균적으로는 N+K이고 K는 무시될 수 있으므로
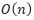
일정한 범위를 가진 Bucket들을 만들어서 Bucket으로 각 데이터를 넣는다. 데이터가 들어있는 Bucket을 정렬하고 각 Bucket에 들어있는 값을 순서대로 합친다. 연결리스트로 버킷을 구성할 수 있고, 버킷들을 정렬할 때는 퀵 정렬 등을 사용한다.
▶ Counting Sort
시간복잡도는 N + K이지만 K는 무시될 수 있으므로
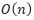
정렬하고자 하는 데이터들의 값이 특정한 범위 안에 있을 떄, 각 데이터들에 정수 Key값을 할당하여 해당 Key값으로 정렬한다.
▶ 힙 정렬 Heap Sort
시간복잡도는 항상 일정한
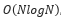
우선순위 큐의 하나인 최대 힙을 사용한다. 가장 큰 원소를 효율적으로 선택할 수 있다. 힙은 완전 이진 트리를 사용하므로 배열을 통해서 표현할 수 있다. 배열로 힙을 만든 다음 데이터를 삭제하고 힙을 재구성하는 과정을 반복한다. 이때 삭제된 노드들을 배열에 차례로 저장하면 정렬된 리스트가 된다.
'알고리즘 스터디_개념정리' 카테고리의 다른 글
| 깊이 우선 탐색 DFS, 너비 우선 탐색 BFS (0) | 2020.08.23 |
|---|---|
| 동적 계획법( DP - Dynamic Programming ), 메모이제이션( Memoization ) (0) | 2020.08.23 |
| 탐욕 알고리즘 Greedy Algorithm + A* Search Algorithm (1) | 2020.08.17 |
| 완전 탐색 알고리즘 - Brute Force (1) | 2020.08.17 |
| 스택, 큐, 힙 (0) | 2020.08.10 |

